Why “vibe physics” is the ultimate example of AI slop

The most fundamental of all the sciences is physics, as it seeks to describe all of nature in the simplest, most irreducible terms possible. Both the contents of the Universe, as well as the laws that govern it, are at the heart of what physics is, allowing us to make concrete predictions about not only how reality will behave, but to accurately describe the Universe quantitatively: by telling us the amount, or “how much” of an effect, any physical phenomenon or interaction will cause to any physical system. Although physics has often been driven forward by wild, even heretical ideas, it’s the fact that there are both

• fundamental physical entities and quantities,
• and also fundamental physical laws,

that enable us to, quite powerfully, make accurate predictions about what will occur (and by how much) in any given physical system.

Over the centuries, many new rules, laws, and elementary particles have been discovered: the Standard Models of both particle physics and cosmology have been in place for all of the 21st century thus far. Back in 2022, the first mainstream AI-powered chatbots, known as Large Language Models (or LLMs), arrived on the scene. Although many praised them for their versatility, their apparent ability to reason, and their often surprising ability to surface interesting pieces of information, they remained fundamentally limited when it comes to displaying an understanding of even basic ideas in the sciences.

Here in 2025, however, many are engaging in what’s quickly becoming known as vibe physics: engaging in deep physics conversations with these LLMs and (erroneously) believing that they’re collaborating to make meaningful breakthroughs with tremendous potential. Here’s why that’s completely delusional, and why instead of a fruitful collaboration, they’re simply falling for the phenomenon of unfettered AI slop.

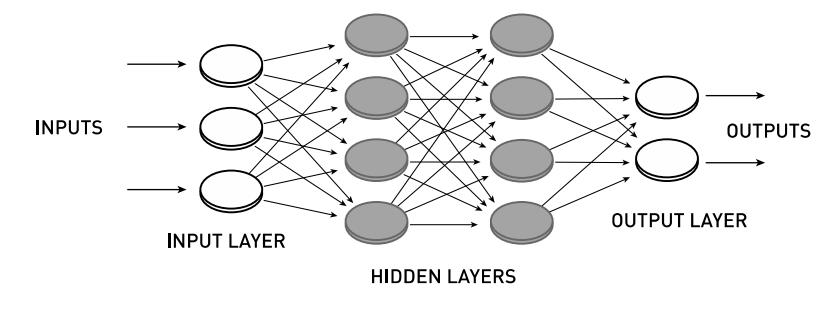
This example of a feedward network (without backpropagation) is an example of a restricted Boltzmann machine: where there is at least one hidden layer between the input layer and the output layer, and where nodes are only connected between different layers: not between nodes of the same layer, representing a tremendous step forward in creating today’s AI/LLM systems.

There are, to be sure, a tremendous number of things that AI in general, and LLMs in particular, are exceedingly good at. This is due to how they’re constructed, which is something that’s well-known but not generally appreciated. While a “classical” computer program involves:

• a user giving an input or a series of inputs to a computer,
• which then conducts computations that are prescribed by a pre-programmed algorithm,
• and then returns an output or series of outputs to the user,

the big difference is that an AI-powered program doesn’t perform computations according to a pre-programmed algorithm. Instead, it’s the machine learning program itself that’s responsible for figuring out and executing the underlying algorithm.

What most people fail to recognize about AI in general, and LLMs in particular, is that they are fundamentally limited in their scope of applicability. There’s a saying that “AI is only as good as its training data,” and what this generally means is that the machine learning programs can be extremely powerful (and can often outperform even expert-level humans) at performing the narrow tasks that they are trained on. However, when confronted with questions about data that falls outside of what they’re trained on, that power and performance doesn’t generalize at all.

Based on the Kepler lightcurve of the transiting exoplanet Kepler-1625b, we were able to infer the existence of a potential exomoon. The fact that the transits didn’t occur with the exact same periodicity, but that there were timing variations, was our major clue that led researchers in that direction. With large enough exoplanet data sets, machine learning algorithms can now find additional exoplanet and exomoon candidates that were unidentifiable with human-written algorithms.

As an example, you can train your AI on large data sets of human speech and conversation in a particular language, the AI will be very good at spotting patterns in that language, and with enough data, can become extremely effective at mimicking human speech patterns and conducting conversations in that language. Similarly, if you trained your AI on large data sets of:

• images of Causasian human faces,
• images of spiral galaxies,
• or on gravitational wave events generated by black hole mergers,

you could be confident that your artificial intelligence algorithm would be quite good at spotting patterns within those data sets.

Given another example of a similar piece of data, your AI could then classify and characterize it, or you could go an alterative route and simply describe a system that had similar properties, and the well-trained AI algorithm would do an excellent job of generating a “mock” system that possessed the exact properties that you described. This is a common use of generative AI, which succeeds spectacularly at such tasks.

With a large training data set, such as a large number of high-resolution faces, artificial intelligence and machine learning techniques can not only learn how to identify human faces, but can generate human faces with a variety of specific features. This crowd in Mauerpark, Berlin, would provide excellent training data for the generation of Caucasian faces, but would perform very poorly if asked to generate features common to African-American faces.

However, that same well-trained AI will do a much worse job at identifying features in or generating images of inputs that fall outside of the training data set. The LLM that was trained on (and worked so well in) English would perform very poorly when presented with conversation in Tagalog; the AI program that was trained on Caucasian faces would perform poorly when asked to generate a Nigerian face; the model that was trained on spiral galaxies would perform poorly when given a red-and-dead elliptical galaxy; the gravitational wave program trained on binary black hole mergers would be of limited use when confronted with a white dwarf inspiraling into a supermassive black hole.

And yet, an LLM is programmed explicitly to be a chatbot, which means one of its goals is to coax the user into continuing the conversation. Rather than be honest with the user about the limitations of its ability to answer correctly given the scope of its training data, LLMs confidently and often dangerously misinform the humans in conversation with them, with “therapist chatbots” even encouraging or facilitating suicidal thoughts and plans.

Still, the success of LLMs in areas where they weren’t explicitly trained, such as in vibe coding, has led to people placing confidence in those same LLMs to perform tasks where their utility hasn’t been validated.

This graphical hierarchy of mathematical spaces goes from the most general type of space, a topological space, to the most specific: an inner product space. All metrics induce a topology, but not all topological spaces can be defined by a metric; all normed vector spaces induce a metric, but not all metrics contain normed vector space; all inner product spaces induce a norm, but not all normed vector spaces are inner product spaces. Mathematical spaces play a vital role in the math powering artificial intelligence.

To be sure, the concepts of artificial intelligence and machine learning do have their place in fields like physics and astrophysics. Machine learning algorithms, when trained on a sufficiently large amount of relevant, high-quality data, are outstanding at spotting and uncovering patterns within that data. When prompted, post-training, with a query that’s relevant to such a pattern found within that data set, the algorithm is excellent at reproducing the relevant pattern and utilizing it in a way that can match the user’s query. It’s why machine learning algorithms are so successful at finding exoplanets that humans missed, why they’re so good at classifying astronomical objects that are ambiguous to humans, and why they’re good at reproducing or simulating the physical phenomena that’s found in nature.

But now we have to remember the extraordinary difference between describing and deriving in a field like physics. With a large library of training data, it’s easy for an LLM to identify patterns: patterns in speech and conversation, patterns that emerge within similar classes of problems, patterns that emerge in the data acquired concerning known objects, etc. But that doesn’t mean that LLMs are competent at uncovering the underlying laws of physics that govern a system, even with arbitrarily large data sets. It doesn’t mean that LLMs understand or can derive foundational relationships. And it doesn’t mean that LLMs aren’t more likely to “continue a conversation” with a user than they are to identify factually correct, relevant statements that provide meaningful, conclusive answers to a user’s query.

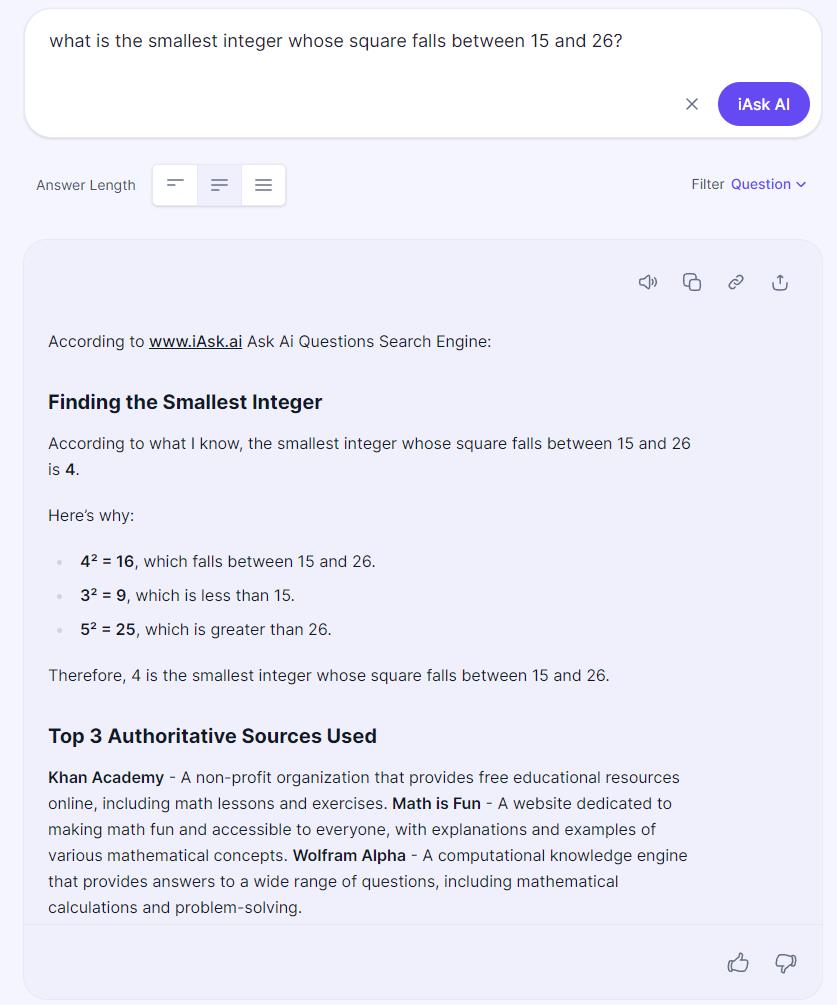
A screenshot from a query about integers directed to iask.ai, along with its woefully incorrect response. The correct answer is -5, which requires inputting several additional prompts to coax the AI into the correct response.

While simply being an expert and conversing with an LLM about physics — or, as an incredible number of scientists and science communicators can attest to, fielding emails from laypersons who’ve been having “vibe physics” conversations with LLMs — easily reveals their limitations and exposes their hallucinations, researchers Keyon Vafa, Peter Chang, Ashesh Rambachan and Sendhil Mullainathan set out to put machine learning systems to a more specific test. In a new paper submitted in July of 2025, the authors sought to test an AI’s ability to infer what they call a foundation model: an underlying law of reality that could then be applied to novel situations that go well beyond the “patterns” found in the AI’s training data.

The way they seek to do this is by generating a large number of new, very small, synthetic data sets. They then challenge the AI’s algorithm to fit a foundation model to those data sets, or in other words, to try and deduce what type of underlying law applies to all of those data sets when aggregated together to explain their behavior. Then, they wanted the AI itself to go and analyze the patterns that it found in those mathematical functions that it deduced, i.e., the foundational model, to search for inductive biases.

Would it find a good foundational model? Would the model be extendable beyond the mere training data? And would it be successful at determining what sort of inductive biases were induced by its choice of model?

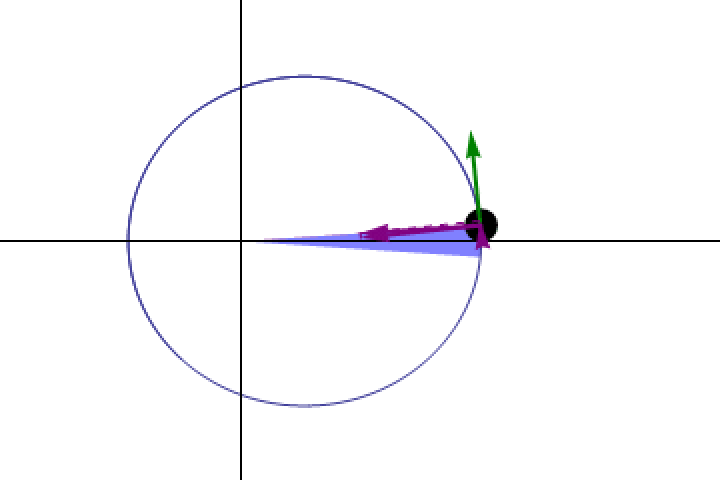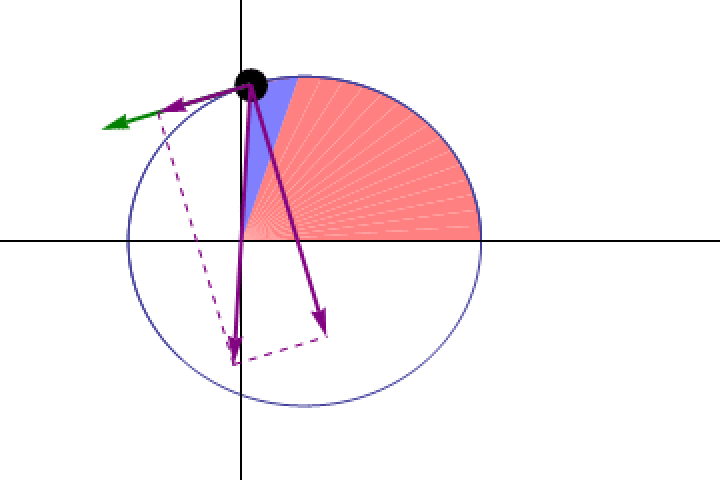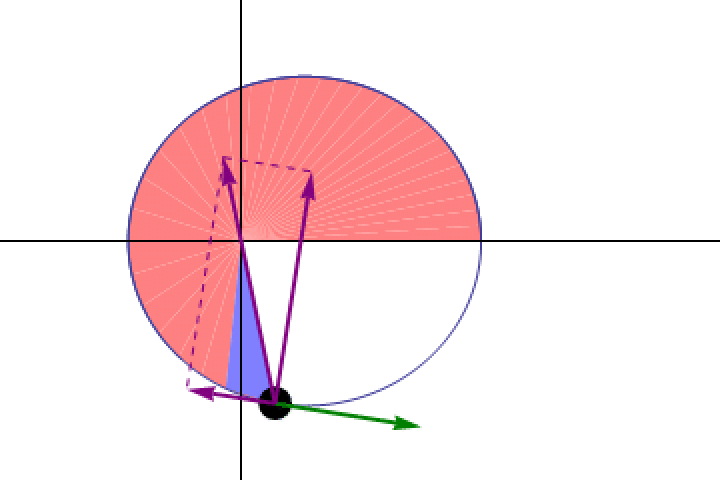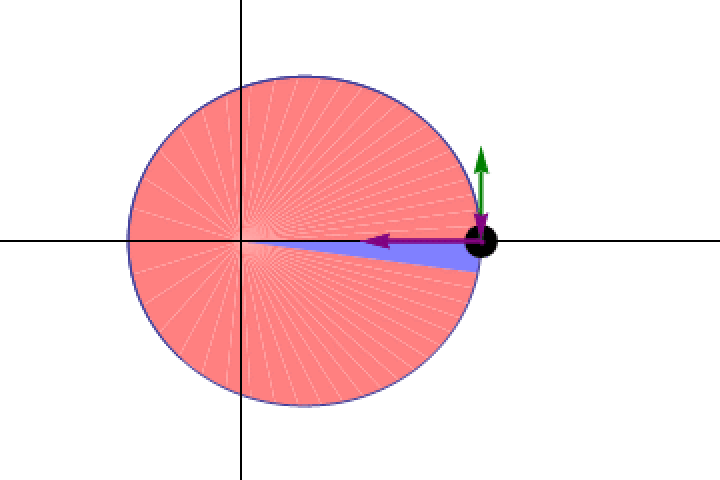
Even before we understood how the law of gravity worked, we were able to establish that any object in orbit around another obeyed Kepler’s second law: it traced out equal areas in equal amounts of time, indicating that it must move more slowly when it’s farther away and more quickly when it’s closer. At every point in a planet’s orbit, Kepler’s laws dictate at what speed that planet must move.

This vocabulary may be difficult for even those well-trained in physics to fully wrap their heads around, so perhaps it’s good to use an example from history to highlight what they’re talking about. One example is the foundational model of Newton’s gravity. Although Newton’s gravity was outstanding for predicting the orbits and motions of the planets, we already had a model for more than half a century prior to Newton that did precisely that: Kepler’s laws. Kepler’s laws were predictive in the sense that you could plunk down a planet at any distance from the Sun, give it an initial velocity, and Kepler’s laws would allow you to know pretty much everything about its orbital properties, even extremely far into the future.

But Kepler’s laws were just predictive laws that worked for one particular set of circumstances: planets in orbit around the Sun. When Newton came up with his law of universal gravitation, they were no different from Kepler’s laws in terms of the predictions they made for planets in motion around the Sun. But Newton’s laws were far more powerful, and represent a foundational model in a way that Kepler’s laws didn’t. The reason is that Kepler’s laws stopped at planets and orbits, but Newton’s also explained:

• the swinging of a pendulum on Earth,
• the motion of moons and satellites around planets,
• the behavior of rockets and the terrestrial motion of projectiles,

and any other situation where gravitation is the ruling phenomenon. Whereas predictions only apply to one set of tasks, foundational models are extendable to many sets of tasks.

This figure shows side-by-side panels for the true force law for planets in our Solar System (blue arrows) and the force laws recovered by an artificial intelligence program given enormous amounts of training data for millions or even billions of synthetic solar systems. Note the complexity, as well as the inconsistency, of the recovered force law using AI.

If you have a wholly new problem involving masses and motions, Newton’s framework gives you a solid starting point, whereas Kepler’s will only give you a solid starting point under a very restrictive set of circumstances; that’s the difference between a predictive model and a foundational model. What the authors of this new paper did was to apply their methodology to three classes of problems: orbital problems (similar to Kepler and Newton), as well as two other (lattice and Othello) problems. As far as predictions went, it was extremely successful, just as Kepler’s predictive model was. Even far into the future, it could reproduce the actual behavior of the system.

But did the model take that leap, and discover Newton’s laws? Did it find the underlying foundational model? Or, perhaps even better, did it find a superior model to Newton’s?

The answer, quite definitively, was no. To demonstrate the model’s failures, they compelled it to predict force vectors on a small dataset of planets: planets within our own Solar System. Instead of discovering the Newtonian phenomenon of centripetal force — a force directed towards the Sun, for planets — they wound up with a very strained, unphysical force law. And yet, because it still gave correct orbits, the model had no way of self-correcting. Even when fine-tuning the model on larger scales, predicting forces across thousands of stellar and planetary systems, it not only didn’t recover Newton’s law; it recovered different, mutually inconsistent laws for different galaxy samples.

When the LLMs o3, Claude Sonnet 4, and Gemini 2.5 Pro were asked to reconstruct force laws for a variety of mock solar systems, they were all unable to recover something equivalent to Newton’s law of universal gravitation, despite the LLMs themselves having been trained on Newton’s laws. It’s stark evidence for how LLMs rely on pattern matching, and are unable to reach even basically valid scientific conclusions about foundational models.

When they then went to put more general models (LLMs) to the same test — like o3, Claude Sonnet 4, and Gemini 2.5 Pro — they added in what a small number (about 2%) of force magnitudes actually were, without explicitly telling the LLM what those forces were, the LLMs couldn’t recover the force law. This is a remarkable failure of generalization and extrapolation, because all three of these LLMs were explicitly trained on Newton’s laws. Even so, they couldn’t get the rest of the forces when prompted to infer the remaining outcomes. In other words, even in the extremely basic scenario of “if I give you the orbits of an enormous number of planets in planetary and stellar systems, can you infer Newton’s law of gravity,” every LLM tested failed spectacularly.

This is the key finding of this new work: you don’t just want to study “can my model predict behavior for a new example of the type of data that the model has been trained on?” Instead, you want to also study behavior on new tasks, where if it did properly learn the foundational model that underlies the observed phenomenon, it would be able to apply it to a novel situation and use that model to make predictions in those new, relevant situations as well. In no cases did the LLMs that we have today do any such thing, which indicates that when you (or anyone) has a “deep conversation” about physics, including about speculative extensions to known physics, you can be completely confident that the LLM is solely giving you patterned speech responses; there is no physical merit to what it states.

While humans are typically regarded as the most intelligent thing to ever arise on planet Earth, many are attempting to create an artificial general intelligence that surpasses human limits. Current attempts to measure or assess the “intelligence” of an AI or an LLM must take care that memorization is not used as a substitute for intelligence.

All of which brings us back to the notion of vibe physics. Sure, an LLM may sound very intelligent and knowledgeable about theoretical physics, particularly if you yourself aren’t an expert in the areas of theoretical physics that you’re discussing with it. But this is exactly the problem any non-expert has when talking with:

• a bona fide, honest, scrupulous expert,
• a dishonest grifter posing as a scrupulous expert,
• or a confident chatbot that has no expertise, but sounds like it does.

The problem is, without the necessary expertise to evaluate what you’re being told on its merits, you’re likely to evaluate it based solely on vibes: in particular, on the vibes of how it makes you feel about the answers it gave you.

This is the most dangerous thing for anyone who’s vested in being told the truth about reality: the potential for replacing, in your own mind, an accurate picture of reality with an inaccurate but flattering hallucination. Rest assured, if you’re a non-expert who has an idea about theoretical physics, and you’ve been “developing” this idea with a large language model, you most certainly do not have a meritorious theory. In physics in particular, unless you’re actually performing the necessary quantitative calculations to see if the full suite of your predictions is congruent with reality, you haven’t even taken the first step towards formulating a new theory. While the notion of “vibe physics” may be alluring to many, especially for armchair physicists, all it truly does is foster and develop a new species of crackpot: one powered by AI slop.