“To consult the statistician after an experiment is finished is often merely to ask him to conduct a post mortem examination. He can perhaps say what the experiment died of.” – Ronald A. Fisher
The modern biology toolbox is larger than ever, as a widening array of cutting-edge molecular techniques supplements the classic approaches that still drive the field forward. Teams of researchers with complementary expertise may combine these tools in countless creative ways to produce novel research. Regardless of which methods are chosen for data collection, all empirical research projects share a common foundation: the principles of good experimental design. Far from eliminating the need for statistical literacy, -omics technologies make careful, sound experimental design more important than ever1,2.
This Perspective was motivated by the observation that many biology projects are doomed to fail by experimental design errors that make rigorous inference impossible. The results of such errors can range from waste to, in the worst case, the introduction of misleading conclusions into the scientific literature, including those with clinical consequences. Our goal is to highlight common experimental design errors and how to avoid them. Although methods for analyzing challenging datasets are improving3,4,5,6, even advanced statistical techniques cannot rescue a poorly designed experiment. For this reason, we focus on choices that must be made before an experiment or study is conducted, rather than on data analysis choices (however, if you are working on microbiomes, we highly recommend that you read this article in conjunction with Willis and Clausen7, who highlight important points for planning and reporting on statistical analyses). In particular, we address four key elements of a well-designed experiment: adequate replication, inclusion of appropriate controls, noise reduction, and randomization.
First, we discuss how in -omics research, many errors arise because of the misconception that a large quantity of data (e.g., deep sequencing or the measurement of thousands of genes, molecules, or microbes) ensures precision and statistical validity. In reality, it is the number of biological replicates that matters. We also explain how to recognize and avoid the problem of pseudoreplication, and we introduce power analysis as a useful method for optimizing sample size. Second, we introduce several strategies (blocking, pooling, and covariates) for minimizing noise, or variation in the data caused by randomness or other unplanned factors. Third, we briefly review how missing positive and negative controls can compromise experimental results, and provide examples from both -omics and non-omics research. Finally, we describe two critical functions of experimental randomization: preventing the influence of confounding factors, and empowering researchers to rigorously test for interactions between two variables.
While these practices are covered in undergraduate and graduate level classes and in textbooks, as reviewers we—along with editors and some colleagues—have observed basic experimental design errors in submitted manuscripts. Indeed, the authors of this Perspective have also made and learned from some of these errors the hard way. This fact inspired this Perspective to provide a succinct overview of important experimental design principles that can be used in training of early-career scientists and as a refresher for seasoned biologists. We present examples from projects that use high-throughput DNA sequencing; however, unlike best methods for statistical analysis, these experimental design principles apply equally to any experiment regardless of the type of data being collected, including proteomics, metabolomics, and non-omics data. We also provide a list of additional resources on the topics discussed (Table 1) and practical steps for designing a rigorous experiment (Box 1).
Empowerment through replication
Many researchers intuitively understand that any individual data point might be an outlier or a fluke. As a result, we have very low confidence in any conclusion that was reached based on one isolated observation. With each additional data point that we collect, however, we get a better sense of how representative that first data point really was, and our confidence in our conclusion grows. Statistics empower us to measure and communicate that confidence in a way that other researchers will understand.
Why biological replication is more important than sequencing depth
Most biologists have heard that having more data will empower them to test their hypotheses. But what does it really mean to have more data? High-throughput technologies that generate millions to billions of DNA sequence reads, and counts of thousands of different genes or microbes, can create the illusion of a big dataset even if the number of replicates, or sample size, remains small. Although deeper sequencing per replicate can improve power in some cases, it is primarily the number of biological replicates that enables researchers to obtain clear answers to their questions.
To illustrate why this is, consider the hypothesis that two species of plants host different ratios of two microbial taxa in their roots. We can estimate this ratio for the two groups or populations of interest (i.e., all existing individuals of the two species) by collecting random samples from those populations. A sample size of 1 plant per species would be essentially useless, because we would have no way of knowing whether that plant is representative of the rest of its population, or instead is an anomaly. This is true regardless of the amount of data we have for that plant; whether it is based on 103 sequence reads or 107 sequence reads, it is still an observation of a single individual and cannot be extrapolated to make inferences about the population as a whole. Similarly, if we measure the abundances of thousands of microbes per plant, this same problem would apply to our estimates for each of those microbes. In contrast, measuring more plants per species will provide an increasingly better sense of how variable the trait of interest is in each population.
To what extent does the amount of data per replicate matter? Deeper sequencing can modestly increase power to detect differential abundance or expression, but those gains quickly plateau after a moderate sequencing depth is achieved3,8. Extra sequencing is most beneficial for the detection of less-abundant features, such as rare microbes or low-expression transcripts, and features with high variance8. Projects that focus specifically on such features will require deeper sequencing than those that do not, or else may benefit from a more targeted approach. Finally, it is worth highlighting the related problem of treating -omics features (e.g., genes or microbial taxa) as the units of replication, as is common in gene set enrichment and pathway analyses. Such analyses describe a pattern within the existing dataset, but they are entirely uninformative about whether that pattern would hold in another group of replicates9. Instead, they only allow inference about whether that pattern would hold for a newly-observed feature in the already-measured group of replicates, which is often not the researcher’s intended purpose.
Replication at the right level
Biological replicates are crucial to statistical inference precisely because they are randomly and independently selected to be representatives of their larger population. The failure to maintain independence among replicates is a common experimental error known as pseudoreplication10 (Box 2). When experimental units are truly independent, no two of them are expected to be more similar to each other than any other two. Pseudoreplication becomes a problem when the incorrect unit of replication is used for a given statistical inference, which artificially inflates the sample size and leads to false positives and invalid conclusions (Fig. 1). In other words, not all data points are necessarily true replicates.
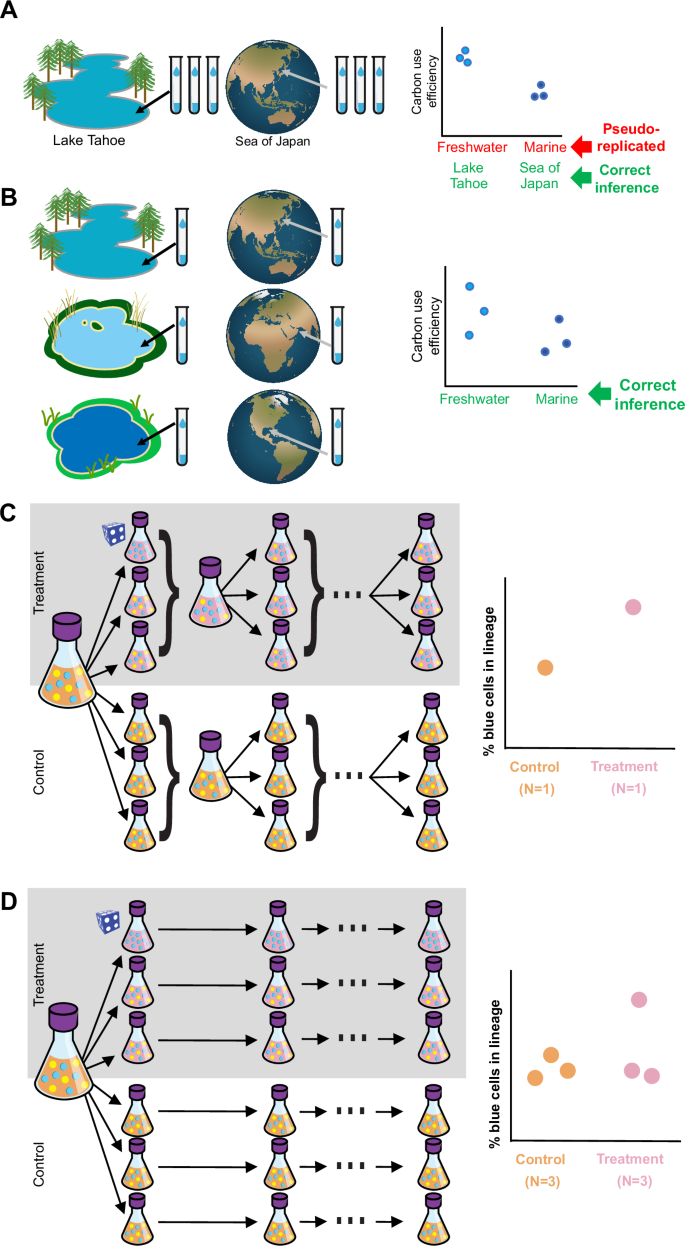
A To test whether carbon use efficiency differs between freshwater and marine microbial communities, a researcher collects three vials from Lake Tahoe and three from the Sea of Japan. This design is pseudoreplicated because the vials from the same location are not independent of each other; they are expected to be more similar to each other than they would be to other vials randomly sampled from the same population (i.e., freshwater or marine). However, they could be used to test the narrower question of whether carbon use efficiency differs between Lake Tahoe and the Sea of Japan, assuming that the vials were randomly drawn from each body of water. B In contrast to the design in panel A, collection of one vial from each of three randomly-selected freshwater bodies and three randomly-selected saltwater bodies enables a valid test of the original hypothesis. Alternatively, each replicate could be the composite or average of three sub-samples per location; this would be an example of pooling to improve the signal:noise ratio. C Pseudoreplication during experimental evolution can lead to false conclusions. Each time that the flasks are pooled within each treatment prior to passaging, independence among replicates is eliminated. As a result, a stochastic event that arises in a single replicate lineage (symbolized by the blue die) can spread to influence the other lineages, so that the stochastic event is confounded with the treatment itself. D In contrast, by maintaining strict independence of the replicate lineages, the influence of the stochastic event is isolated to a single replicate. The researcher can confidently rule out the possibility that a stochastic event has systematically influenced one of the treatment groups.
Although pseudoreplication is occasionally unpreventable (particularly in large-scale field studies), it can and should be anticipated and avoided whenever possible. The correct units of replication are those that can be randomly assigned to receive one of the treatment conditions that the experiment aims to compare. In experimental evolution, for instance, the replicates are random subsets of the starting population, assumed to be identical, each of which may be assigned to a different selective environment11,12. Failure to include enough independent sub-populations, or to keep them independent throughout the experiment (e.g., by pooling replicates; Fig. 1C–D), will cause pseudoreplication of the evolutionary process of interest13. In some cases, however, mixed-effects modeling techniques can adequately account for the non-independence of replicates10.
Optimizing sample size
If most measurements in a dataset are similar to each other, this indicates that we are measuring individuals from a low-variance population with respect to the dependent variable. In contrast, a wide range of trait values signals a high-variance population. This within-group variance (i.e., the variance within one population) is central to determining how many biological replicates are necessary to achieve a clear answer to a hypothesis test: when within-group variance is high relative to the between-group variance, more replicates are required to achieve a given level of confidence (Fig. 2A). However, when the budget for sequencing is fixed, then increasing the sample size is costly—not only because wet lab costs increase, but also because the amount of data per observation decreases. Too many replicates can waste time and money, while too few can waste an entire experiment. How can a biologist know ahead of time how many replicates are enough?
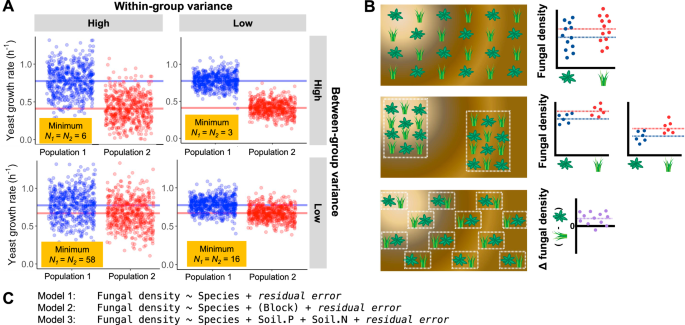
Statistical power depends on both the between-group variance (the signal or effect size) and the within-group variance (the noise). Smaller effect sizes require larger sample sizes to detect, especially when noise is high. A Points show trait values of individuals comprising two populations (used in the statistical sense of the word); horizontal lines indicate the true mean trait value for each population. Thus, the distance between horizontal lines is the effect size. The populations could be two different species of yeast; the same species of yeast growing in two experimental conditions; the wild type and mutant genotypes; etc. To estimate the difference between populations, the researcher can only feasibly measure a subset (i.e., sample) of individuals from each population. The yellow boxes report the minimum sample size per group needed to provide an 80% chance of detecting the difference using a t-test, as determined using power analysis. B Blocking reduces the noise contributed by unmeasured, external factors (e.g., soil quality in a field experiment with the goal of comparing fungal colonization in the roots of two plant species). Soil quality is represented by the background color in each panel. Top: without blocking, soil quality influences the dependent variable for each replicate in an unpredictable way, creating high within-group variance. Middle: spatial arrangement of replicates into two blocks allows estimation of the difference between species while accounting for the fact that trait values are expected to differ between the blocks on average. Bottom: in a paired design, each block contains one replicate from each group, allowing the difference in fungal colonization to be calculated directly for each block and tested through a powerful one-sample or paired t-test. C Three statistical models that could be used in an ANOVA framework to test for the difference in fungal density between plant species, as illustrated in panel B. Relative to Model 1, the within-group variance for each plant species will be reduced in both Model 2 and Model 3. For Model 2, this is accomplished using blocking; a portion of the variance in fungal density can be attributed to environmental differences between the blocks (although these may be unknown and/or unmeasured) and therefore removed from the within-group variances. For Model 3, it is accomplished by including covariates; a portion of the variance in fungal density can be attributed to the concentrations of N and P in the soil near each plant and therefore removed from the within-group variances. Note that for Model 3, the covariates need to be measured for each experimental unit (i.e., plant), rather than each block; in fact, it is most useful when blocking is not an option.
A flexible but underused solution to this problem—power analysis—has existed for nearly a century14,15. Power analysis is a method to calculate how many biological replicates are needed to detect a certain effect with a certain probability, if the effect exists (Fig. 2A). It has five components: (1) sample size, (2) the expected effect size, (3) the within-group variance, (4) false discovery rate, and (5) statistical power, or the probability that a false null hypothesis will be successfully rejected. By defining four of these, a researcher can calculate the fifth.
Usually, both the effect size and within-group variance are unknown because the data have not yet been collected. The choice of effect size for a power analysis is not always obvious: researchers must decide a priori what magnitude of effect should be considered biologically important. Acceptable solutions to this problem include expectations based on the results of small pilot experiments, using values from comparable published studies or meta-analyses, and reasoning from first principles. For example, a biologist planning to test for differential gene transcription may define the minimum interesting effect size as a 2-fold change in transcript abundance, based on a published study showing that transcripts stochastically fluctuate up to 1.5-fold in a similar system. In this scenario, the stochastic 1.5-fold fluctuations in transcript abundance suggest a reasonable within-group variance for the power analysis. As another example, a bioengineer may only be interested in mutations that increase cellulolytic enzyme activity by at least 0.3 IU/mL relative to the wild type, because that is known to be the minimum necessary for a newly designed bioreactor. To determine the within-group variance for a power analysis, the bioengineer could conduct a small pilot study to measure enzyme activity in wild-type colonies. As a final example, if a preliminary PerMANOVA for a very small amount of metabolomics data (say, N = 2 per group) from a pilot study estimated that R2 = 0.41, then a researcher could use that value as the target effect size for which he/she aims to obtain statistical support.
Freely available software facilitates power analysis for basic statistical tests of normally-distributed variables, including correlation, regression, t-tests, chi-squared tests, and ANOVA16,17,18,19. Power analysis for -omics studies, however, is more complex for several reasons. -Omics data comprise counts that are not normally distributed and may contain many zeroes, and some features may be inherently correlated with each other; these properties must be modeled appropriately for a power analysis to be useful20. The large number of features often requires adjustment of P-values to correct for inflated Type I error rates, which in turn decreases power. Furthermore, statistical power varies among features because they differ not only in within-group variance, but also in their overall abundance. In general, more replicates are required to detect changes in low-abundance features than in high-abundance ones8. Statistical power also varies among different alpha- and beta-diversity metrics21 that are commonly used in amplicon-sequencing analysis of microbiomes. For power analysis of multivariate tests (e.g., PERMANOVA), which incorporate information from all features simultaneously to make broad comparisons between groups, simulations are necessary to account for patterns of co-variation among features. In such cases, pilot data or other comparable data are crucial for accurate power analysis.
Fortunately, tools are available to estimate power for common analyses used in proteomics22, RNA-seq3,20,23,24, and microbiome studies21,25,26. Recent reviews27,28 demonstrate this process for various forms of amplicon-sequencing data, including taxon abundances, alpha- and beta-diversity metrics, and taxon presence/absence. They also consider several types of hypothesis tests, including comparisons between groups and correlations with continuous predictors. Although power analysis may seem daunting at first, it is an investment with excellent returns. This skill empowers biologists to budget more accurately, write more convincing grant proposals, and minimize their risk of wasting effort on experiments that cannot generate conclusive results.
Empowerment through noise reduction
As explained above, statistical power is positively related to the sample size and negatively related to the within-group variance. Thus, we can increase power either by including more biological replicates or by reducing within-group variance. Because our budgets do not allow us to increase replication indefinitely, it is useful to consider: What methods exist to increase power by decreasing within-group variance?
A classic way to minimize within-group variance is to remove as many variables as possible29. Common examples include using a single strain instead of multiple; strictly controlling the lab environment; and using only male host animals30. Such practices minimize noise, or variance contributed by unplanned, unmeasured variables. However, they come with a drawback: the loss of generalizability30,31,32. If a mutation’s phenotype cannot be detected in the face of minor environmental variation, is it likely to be relevant in nature? If an interesting function occurs only in a lab strain, is it important for the species in general? Such limitations should always be considered when interpreting results.
Another technique to reduce within-group variance is blocking, the physical and/or temporal arrangement of replicates into sets based on a known or suspected source of noise (Fig. 2B). For instance, clinical trials may block by sex, so that results will be based on comparisons of males to males and females to females. Crucially, all experimental treatments must be randomly assigned within each block. Blocking is also useful for large experiments with more replicates than can be measured at once; as long as the replicates within each block are treated identically, sources of noise such as multiple observers can be controlled. The most powerful form of blocking is paired design, in which experimental units are kept in pairs from the beginning. One unit per pair is randomly assigned to the treatment group, the other to the control; the difference between units is then calculated directly, automatically accounting for sources of noise that are shared within the pair (Fig. 2B, bottom panel). A possible downside of highly-structured blocking designs is that they can complicate the re-use of the data to answer questions other than the one for which the design was optimized, whereas a simple randomized design is highly flexible but not optimized for any particular purpose.
When sources of noise are known beforehand, they ideally should be measured during the experiment so that they can be used as covariates. A covariate is any independent variable that is not the focus of an analysis but might influence the dependent variable. When using regression, ANOVA, or similar methods, one or more covariates may be included in the statistical model to control for their effects on the variable of interest (Fig. 2C). For instance, controlling for replicates’ spatial locations can dramatically reduce noise in field studies33,34. Similarly, dozens of covariates related to lifestyle and medical history contribute to the variation in human fecal microbiome composition35. The authors showed that by controlling for just three of these covariates, the minimum sample size needed to detect a microbiome contrast between lean and obese individuals would decrease from 865 to 535 individuals per group.
Finally, pooling–combining two or more replicates from the same group prior to measurement–can reduce within-group variance and the influence of outliers36. For example, pooling RNA can empower biologists to detect differential gene expression from fewer replicates, reducing costs of library preparation and sequencing37. This approach is especially helpful for detecting features that are low-abundance and/or have large within-group variance. Its main drawbacks are that it reduces sample size and results in the loss of information about specific individuals, which may be necessary for unambiguously connecting one dataset to another or linking the response variable to covariates. In fact, excessive or unnecessary pooling is a common experimental design error that can eliminate replication (Fig. 1C–D; Box 2), but is easily avoided by remembering that the pools themselves are the biological replicates.
Empowerment through inclusion of appropriate controls
Key to any experimental design is the inclusion of appropriate positive and negative controls to strengthen conclusions and enable correct interpretation of the experimental results (Box 2). Positive controls can confirm that experimental treatments and measurement approaches work as expected. Positive controls can, for example, be samples with known properties that are carried through a procedure from start to end alongside the experimental samples. For microbiome-related protocols, mock community samples can often be a good positive control38. In addition to serving as positive controls, spike-ins can serve as internal calibration and normalization standards39,40. Negative controls allow detection of artifacts introduced during the experiment or measurement. Negative controls can be samples without the addition of the organism/analyte/treatment of interest that are carried alongside the experimental samples through all experimental steps. They often reveal artifacts caused by the matrix/medium in which samples are embedded; for example, to analyze secreted proteins in the culture supernatant of a bacterium, measuring the proteins in non-inoculated culture medium would be a critical negative control. In microbiome and metagenomics studies, negative controls are particularly crucial when working with low-biomass samples because contaminants from reagents can become prominent features in the resulting datasets41.
Empowerment through randomized design
The random arrangement of biological replicates with regards to space, time, and experimental treatments is a crucial research practice for several reasons.
Randomization protects against confounding variables
For a given level of replication, the researcher must decide how to distribute those replicates in time and space. The importance of randomization—the arrangement of biological replicates in a random manner with respect to the variables being tested—has long been appreciated in ecology, clinical research, and other fields where external influences are impossible to control. Even in relatively homogenous lab settings, failure to randomize can lead to ambiguous or misleading results. This is because randomization minimizes the possibility that unplanned, unmeasured variables will be confounded with the treatment groups42. Unlike experimental noise—random deviations that decrease power by increasing variance—confounding variables cause a subset of replicates to deviate systematically from the others in a way that is unrelated to the intended experimental design. Thus, they cause biased results. Fortunately, confounding variables that are structured in time and/or space can be controlled through randomization (Fig. 3). Even for complex experimental designs, randomization can be easily achieved by sorting a spreadsheet based on a randomly generated number to assign the position of each replicate. In a fully randomized design, all replicates in an experiment are randomized as a single group. In structured designs such as an experiment that employs blocking (see “Empowerment through noise reduction”), however, the best approach is to randomize the replicates within each block, independently of the other blocks.
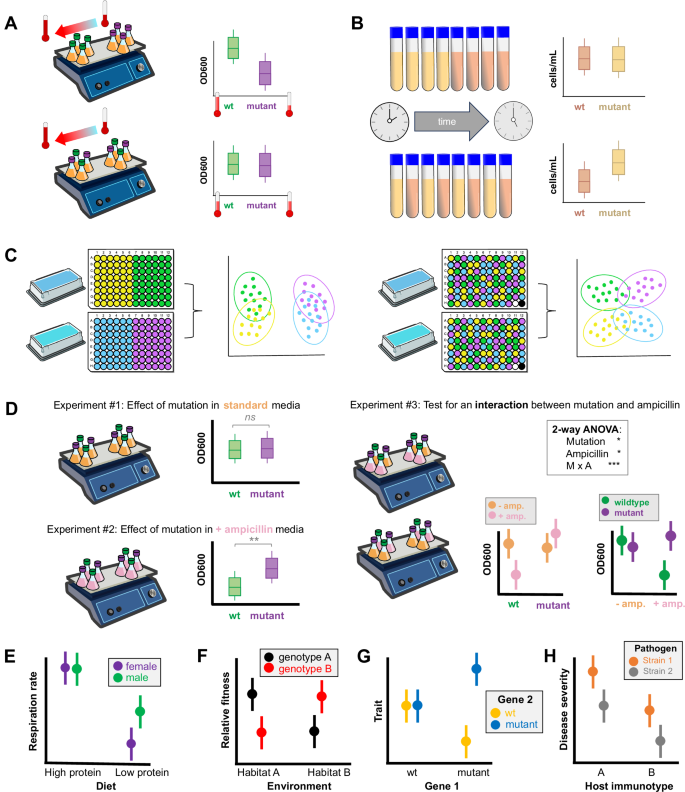
A Top: An undetected temperature gradient within a lab causes a false positive result. The mutant strain grows more slowly than the wild-type on the cooler side of the lab. Bottom: After randomizing the flasks in space, temperature is no longer confounded with genotype and the mutation is revealed to have no effect on growth. B Top: A chronological confounding factor causes a false negative result. When cells are counted in all of the rich-media replicates first, the poor-media replicates systematically have more time to grow, masking the treatment effect. Other external variables that can change over time include the lab’s temperature or humidity, the organism’s age or circadian status, and researcher fatigue. Bottom: Randomizing the order of measurement eliminates the confounding factor, revealing the treatment effect. C Left: Batch effects exaggerate the similarity between the yellow and green groups and between the purple and blue groups. Right: Randomization of replicates from all four groups across batches leads to a more accurate measurement of the similarities and differences among the groups. Inclusion of positive and negative controls (black and white) can help to detect batch effects. D Randomization is necessary to test for interactions. Left: In hypothetical Experiments 1 and 2, one variable (genotype) is randomized but the other (ampicillin) is not. These observations, separated in time and/or space, cannot be used to conclude that ampicillin influences the effect of the mutation. Right: Both variables (genotype, ampicillin) are randomized and compared within a single experiment. A 2-way ANOVA confirms the interaction and the conclusion that ampicillin influences the mutation’s effect on growth is valid. The two plots displaying the interaction are equivalent and interchangeable; the first highlights that the effect of the mutation is apparent only in the presence of ampicillin, while the second highlights that ampicillin inhibits growth only for the wild-type strain. E–H illustrate other patterns that can only be revealed in a properly randomized experiment. E A low-protein diet reduces respiration rate overall, but that effect is stronger for female than male animals. F Two plant genotypes show a rank change in relative fitness depending on the environment in which they are grown. G Two genes have epistatic effects on a phenotypic trait: a mutation in Gene 1 can either increase or decrease trait values depending on the allele at Gene 2. H This plot shows a lack of interaction between the pathogen strain and the host immunotype, as indicated by the (imaginary) parallel line segments that connect pairs of points. In contrast, the line segments that would connect pairs of points would not be parallel if an interaction were present (see E–G). In H, host immunotype A is more susceptible to both pathogen strains than host immunotype B, and pathogen strain 1 causes more severe disease than strain 2 regardless of host. Image credits: vector art courtesy of NIAID (orbital shaker) and Servier Medical Art (reservoir).
Projects using -omics techniques are particularly vulnerable to batch effects, a common type of confounding variable with the potential to invalidate an experiment1,43,44,45,46 (Fig. 3C). When not all replicates can be processed simultaneously, they must be divided into batches that often vary in their exposure to not only chronological factors but also variation among reagent lots, sequencing runs, and other technical factors. While batch effects can be minimized through careful control of experimental conditions, they are difficult to avoid entirely. Although some tools are available to cleanse datasets of batch-related patterns47, the biological effect cannot be disentangled from the batch effect if the two are severely confounded. Therefore, it is always wise to randomize replicates among analytical batches (Fig. 3C).
Randomization allows testing for interactions
Finally, randomization is necessary to rigorously test for interactions between experimental factors (Fig. 3D–H). An interaction is present if one independent variable moderates the effect of another independent variable on the dependent variable. Examples of interactions include epistasis between genes, temperature influencing the phenotypic effect of a mutation, and host genotypes differing in susceptibility to a pathogen.
Many biologists are interested in such context-dependency, but proper experimental design is crucial for testing interactions rigorously. It can be tempting to conduct a series of simple trials that alter one variable at a time and then compare the results of those trials; however, this approach is invalid for testing interactions48. Instead, when multiple independent variables are of interest, the biological replicates must be randomized with respect to all of them, simultaneously (Fig. 3D).
Occasionally full randomization is impossible and the experiment may require a split-plot design, where one variable is randomly assigned to groups of replicates rather than individual replicates. For instance, tubes cannot be randomized with respect to temperature within a single incubator; therefore, they must be distributed across multiple incubators, each of which is randomly assigned to a temperature treatment. The main challenge of split-plot designs is that two plots can differ from each other in ways other than the applied treatment, leading to uncertainty about any observed effects of the treatment. In the above scenario, to minimize the possibility that unintentional differences between incubators are the true cause of any observed differences, ideally at least 2 incubators would be used per temperature (either in parallel or in sequential replications of the experiment). As long as the tubes are randomized within incubators with respect to other variables, tests for interactions are valid. However, split-plot designs have less statistical power than fully-randomized designs.
Source link