Could “positive geometry” unlock the theory of everything?

When most scientists talk about progress in their field, they speak about small, incremental changes that slightly, gradually improve our understanding of how the Universe works. But when we think about the biggest advances in scientific history, they often occur in revolutionary leaps, completely overthrowing our previously held views of how the Universe works. In particular, revolutions like Special Relativity and General Relativity, quantum mechanics and quantum field theory, and the Big Bang and cosmic inflation completely overthrew our prior picture of how things actually behave. As the “holy grail” of physics, many have long sought a Theory of Everything, seeking to explain every particle, phenomenon, and interaction in all the Universe within a single framework, and possibly even with a single equation.

Many attempts have famously been made in the past. Theodor Kaluza added extra dimensions, attempting to unify gravity with electromagnetism. Bryce DeWitt and John Wheeler pioneered approaches to a quantum theory of gravity. A slate of physicists, including Howard Georgi and Shelly Glashow, proposed unifying all the forces of the Standard Model in Grand Unified Theories. And string theory seeks an even grander prize, as an attempt at a true Theory of Everything. Thus far, these (and similar) ideas have failed to lead to a discovery of new physics, or to observations that bear out their predictions. But could that all change with the field of positive geometry? That’s what Stephen Johnson wants to know, asking:

“[W]hat’s going on with positive geometry and is it worth paying attention to? Could the young field… find a theory of everything?”

There’s no shame in taking a big swing when it comes to any endeavor in life, and attempts at a Theory of Everything certainly count as swinging for the fences. Positive geometry has a chance, but it’s got a long road ahead of it. Here’s why.

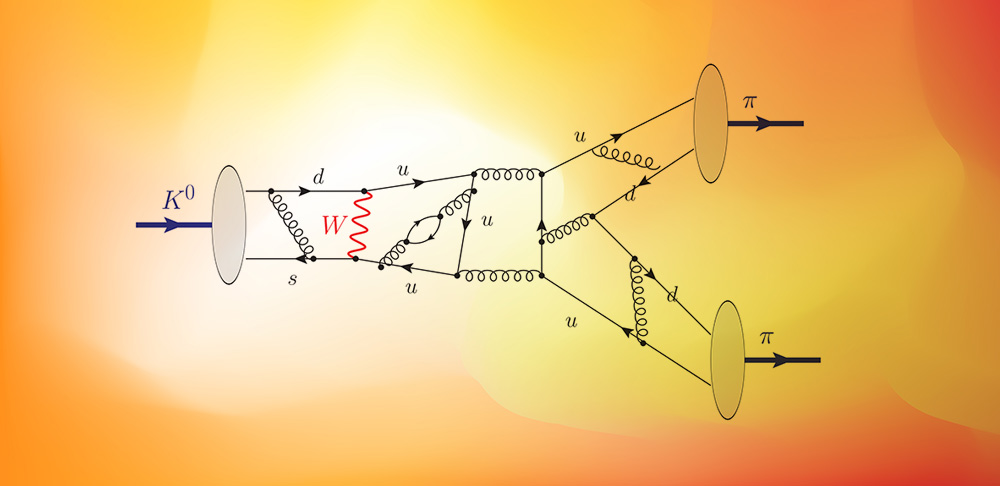
When the neutral kaon (containing a strange quark) decays, it typically results in the net production of either two or three pions. Supercomputer simulations are required to understand whether the level of CP-violation, first observed in these decays, agrees or disagrees with the Standard Model’s predictions. With the exception of only a few particles and particle combinations, almost every set of particles in the Universe are unstable, and if they don’t annihilate away, they will decay in short order.

When it comes to the particles and interactions that govern the Universe — at least, as we understand the Universe today — there are two separate, and incompatible, ways that we presently make sense of our physical reality.

• On the side of gravitation, we have Einstein’s General Relativity: our classical theory of gravity, where mass-and-energy curve the fabric of spacetime, including allowing it to expand or contract, and that curved spacetime then dictates how matter and energy move through that spacetime.
• And over on the side of particle physics, we have the Standard Model of elementary particles, dictating the properties of the quarks, leptons, and known bosons present in the Universe, as well as the interactions that occur between them: the electromagnetic, weak nuclear, and strong nuclear forces.

We know how to perform all of our calculations in both of these frameworks: in General Relativity for problems involving gravitation, and within Quantum Field Theory (using the background spacetime dictated by General Relativity) for problems involving the other three forces. This allows us to calculate most of the phenomena that occur in our Universe, but there are a few gaps in what we can explain, which further motivates the quest for a better, more comprehensive theory. (In other words, for a Theory of Everything.)

It’s generally assumed that at some level, gravity will be quantum, just like the other forces. While the semi-classical approximation for computing the decay of black holes involves performing quantum calculations in the classical background of Einstein’s curved space, that approach might not be valid for capturing the full suite of physical behavior that the outgoing radiation possesses, particularly as far as information is concerned.

We don’t know what dark matter or dark energy is, nor do we know why our Universe has more matter than antimatter. We don’t know why the Standard Model particles have the masses that they do, or why those masses are so much lower than the Planck scale. We don’t know, when a particle goes through a double slit, how its gravitational field behaves. And we don’t know, when you get very close to a very dense source of mass, like a black hole, how any of the fundamental forces behave. It is greatly hoped that a new theory, one superior to our present understanding, might empower us to solve these current puzzles, and to usher in a new era where we understand the Universe in ways that are mysterious to us today.

To be sure, many approaches have been tried in the past, but all sorts of predictions that arose from them have yet to be validated or borne out by experiment. Some of those novel predictions include:

• proton decay,
• neutrinoless double beta decay,
• the existence of new particles, detectable at colliders, beyond the Standard Model,
• evidence for extra dimensions,
• evidence for flavor-changing neutral currents,
• evidence for compositeness to the Higgs boson, or of multiple Higgs bosons,
• baryon number-violating interactions,

and several other exciting quests at the frontiers of physics. Unfortunately, all of our experimental and observational searches for these predicted phenomena have come up empty, placing strong constraints on how our Universe actually behaves on a more fundamental level.

The central idea of String Theory is that all the quanta we know of are described by tiny strings that vibrate in various ways on minuscule scales: far below what’s ever been probed. String theory is an attempt at a framework for quantum gravity, and arguably the only viable candidate for finding out what’s real in the Universe on trans-Planckian scales.

Most people assume that, if a Theory of Everything exists, it will have a certain set of properties. It’s assumed that the Universe is inherently quantum in nature, and that it will be possible to formulate a quantum theory of gravity, placing gravitation on the same footing as the other three inherently quantum forces. It’s assumed that there are more relationships, and deeper (mathematical) connections, between the particles that are known to exist in the Universe. It’s assumed that the unexplained phenomena we have today, like dark matter and dark energy (among others), are indirect evidence that there are new particles, and perhaps a spectrum of new particles, beyond the Standard Model.

But we can’t just write down anything we like in an attempt to cook up a grander theory that encompasses all of what’s known along with all of these assumptions. We also have to be constrained by physical reality, including from all the exquisite existing data from particle colliders like Fermilab and the Large Hadron Collider, that tell us which extensions to the Standard Model are ruled out. And then, we have to face the task that brings us the greatest difficulty: we have to figure out how to calculate what novel contributions our Theory of Everything predicts, in a quantitative fashion, that connects to our actual physical observables.

Today, Feynman diagrams are used in calculating nearly every fundamental interaction spanning the strong, weak, and electromagnetic forces, including in high-energy and low-temperature/condensed conditions. The electromagnetic interactions, shown here, are all governed by a single force-carrying particle: the photon, and can result in interactions that are attractive, repulsive, or “other” despite being mediated by the same type of particle.

You might, when you hear about quantum field theories, think about something akin to the above: where we sum up large numbers of Feynman diagrams, or pathways that describe all the possible interactions between certain sets of particles, to calculate how particles interact. Although this is correct in a sense — it is indeed how most calculations are performed in quantum electrodynamics and in calculations of the weak interactions — this technique has a fundamental limit in how useful it can be.

• One limit is set by the strength of the coupling: this technique works well for forces like electromagnetism and the weak nuclear force, where the coupling is small, and where calculating greater numbers of more complex diagrams brings you closer and closer to the actual, physical answer.
• And a second limit is set by the method itself: you can’t get arbitrarily close to the exact answer by calculating progressively more and more terms. Eventually, you will run into the limitation that the Feynman diagram approach doesn’t give you a convergent series of terms, but rather an asymptotic series. Beyond a certain number of calculated terms, even though that number may be very large, performing more complex calculations will actually leave you farther from the answer than by truncating your series of diagrams at an earlier point.

The way to avoid these limitations isn’t to abandon quantum field theory, but rather to go beyond the perturbative approach of Feynman diagrams, and to perform the full analytic calculations demanded by the underlying quantum field theory.

This depiction of a lattice QCD method shows that space and time are discretized into a set of grid-like points on a lattice. As the spacing between points decreases and the overall size of the lattice tends toward infinity, the true value for QCD calculations is approached more and more accurately.

For the strong nuclear force, for example, we have the technique of Lattice QCD, which was developed because the Feynman diagram technique is wholly ineffective for calculating what’s observable. The strength of the strong force’s coupling is the culprit here, as it’s so great that calculating Feynman diagrams to even one-loop order takes you farther from the correct answer than simply calculating the simple tree-level approximation. So instead, we formulate a gauge theory on a grid (i.e., a lattice) of points in space and time, making the lattice as large as possible and the space between the lattice points as small as possible. As our computational power advances, so does the precision of Lattice QCD.

But that’s not a Theory of Everything; that’s just a way to calculate things within the Standard Model. However, both Lattice QCD and conventional Feynman diagram calculations have something in common that’s very important: they empower scientists to connect a very intensely mathematical framework (the underlying quantum field theory) with the quantities that are actually observable and measurable.

When physicists (and laypersons) often talk about Theories of Everything or quantum field theories in general, they tend to lose sight of what those observables are. And in most cases, they’re dominated by two things:

• cross-sections, or the likelihood of having a specific process take place during a scattering interaction,
• and scattering amplitudes, or the probability of the outgoing quantum wave being related to the incoming plane wave of the pre-interaction particle.

When a heavy lepton (like the tau, shown here) decays, it can decay to two pions through both real (b, c) and virtual (a) processes. There are also scattering (d) effects that can take place. Computing these decays requires understanding the contributions of the strong force (including all quarks and gluons) to the intermediate components of these diagrams, which is difficult for both the tau and the muon. In particle physics, calculating scattering amplitudes and cross-sections are particularly relevant for linking theory with experiment.

It’s with these aspects of theoretical physics in mind that the field of positive geometry is of great interest to physicists and mathematicians. What you see, above, is a visualization of a mathematical structure known as the amplituhedron. (Yes, it’s a mouthful, but there’s a reason for the name!) An amplituhedron is a mathematical, geometric structure that was introduced by two researchers — Nima Arkani-Hamed and Jaroslav Trnka — who were actually working on calculating scattering amplitudes in quantum field theories: in gauge theories in particular.

One underappreciated aspect of scattering amplitudes is that there is a simplicity to them in the sense that there are symmetries to them, but those symmetries aren’t readily apparent in the typical “write down Feynman diagrams, calculate them, and sum them together” approach. In order to normalize a scattering amplitude when using Feynman diagrams, you have to perform a number of sophisticated mathematical tricks, such as:

• renormalization to ensure the the probabilities of all your possible outcomes adds up to 1 (a feature known as unitarity),
• and to impose external conditions, such as locality, so that you don’t have interactions between two different regions of the Universe that couldn’t affect one another unless information was being transmitted faster than the speed of light.

One of the very attractive features of the amplituhedron, one that was noticed right away by Arkani-Hamed and Trnka, was that these two features, unitarity and locality, are necessary (but not fundamental) consequences that can be derived by using the amplituhedron framework.

This sketch shows a three-dimensional face of the four-dimensional amplituhedron for the case of 8 total components. The paper from which this diagram was taken, made public in 2013 and published in 2014, represents the debut of the amplituhedron structure.

The amplituhedron is, admittedly, motivated by many of the ideas in string theory, as it applies not to the Standard Model, but to the maximally supersymmetric N = 4 super-Yang-Mills vector space. The mathematical foundation for these superspaces, on which supersymmetry is constructed, are Grassmann numbers, which themselves are elements of the exterior algebras defining complex vector spaces. That’s where the connection is between physics and mathematics:

• physicists are interested in calculating scattering amplitudes,
• the amplituhedron is a geometric structure that enables and facilitates some of those calculations,
• where the (very interesting to string theorists) N = 4 supersymmetric Yang-Mills theory corresponds (is equivalent to) a certain model of string theory in twistor space,
• and where the amplituhedron is connected to cluster algebras and the positive Grassmannian in n-dimensional spaces (rather than restricted to the 3-dimensions we’re accustomed to) on the mathematical side.

In fact, when people talk about “positive geometry” it’s exactly that mathematical side of this connection that they’re looking at, while physicists are generally more interested in the observables (i.e., the scattering amplitudes) that can be calculated by using it. Unsurprisingly, there are many who work on both aspects of the amplituhedron/positive geometry, and several prominent conferences and workshops have been devoted to this connection since its introduction in 2013.

This mathematical structure is a higher-dimensional geometrical object designed to visualize the amplituhedron. If you can calculate the volume of the projected faces of selected edges, you can know the scattering amplitude of the corresponding system: a tremendous mathematical advance with extreme relevance, at least in principle, to physical system.

This is a remarkable way that could potentially enable physicists to reformulate quantum field theories in terms of geometry, which is one of the main pathways people have considered for unifying General Relativity with quantum field theory, and as a candidate way to arrive at a Theory of Everything. The amplituhedron is an incredibly powerful calculational tool, enabling those who work with them to compute — by hand, mind you — scattering amplitudes for problems that could not have been feasibly calculated even by a computer beforehand. It provides a much simpler tool for performing these key calculations than had ever been available to physicists working on these types of problems beforehand.

It’s the kind of theoretical development that physicists salivate over, and the “nicety” that unitarity and locality just pop out of this approach, naturally, has instigated a wave of thought in physics that perhaps these are not fundamental properties of nature, but rather are emergent properties of the underlying geometry that shapes our reality. If you were trained on conventional physics (like I was), you probably think of scattering as a process that emerges from:

• particles,
• with certain positions at certain times,
• interacting in some fashion over some interval,
• and then leading to outgoing particles with specific positions and momenta at later times,

it might come as a surprise to see a completely different approach. But in positive geometry, which is based in the type of space described by Roger Penrose’s twistor theory from 1967, just a simple set of terms can be written down, and calculated in a straightforward fashion, that yield a geometric object whose volume components can be calculated. That’s what the positive Grassmannian is, and that’s where the connection between the mathematics of positive geometry and the physics of scattering amplitudes comes in.

Although this picture looks very different from a conventional Feynman diagram, and also doesn’t look very much like a conventional geometric object, it encodes a framework, within the field of positive geometry, for calculating the scattering amplitude of a many-particle interacting system. This on-shell diagram helps connect the mathematics of Grassmannian manifolds with scattering amplitudes.

In the 12 years since the amplituhedron was first pointed out and leveraged for calculational purposes, many further advances have occurred: mostly on the mathematical side, which is a generally underappreciated aspect of how physics theories develop. In particular, key developments in the mathematical tools surrounding:

• algebraic geometry,
• combinatorics,
• and the theory of D-modules,

are all helping the field of positive geometry flourish, and leading many to uncover surprising connections to the world of physics, from particle physics to cosmology.

Yes, that’s right: in cosmology as well. Sure, we might live in a Universe with three spatial dimensions and one time dimension, and the field of positive geometry works explicitly in higher-dimensional mathematical spaces only. But by representing what we traditionally (in physics) consider as “interactions” in terms of volumes of higher-dimensional geometric objects, including the amplituhedron, a new type of calculational power can be tapped into. Cosmological polytropes, themselves positive geometries, can help physicists understand what types of signatures might appear in leftover relics from the Big Bang — including the large-scale galaxy distribution in the cosmos and the light from the cosmic microwave background — to learn about and reconstruct the physical laws that led to the birth of our Universe as we know it.

As mathematicians Claudia Fevola and Anna-Laura Sattelberger, who work on the math side of this problem, wrote earlier this year, “It is now up to the scientific community to work out the details of these emerging mathematical objects and theories and to validate them.” In other words, yes, it’s worth paying attention to, and it could potentially lead us to a theory of everything. However, it could also lead us nowhere but down a new blind alley. The only way to know which way it’ll turn out is to explore it fully, allowing nature to ultimately decide.

Send in your Ask Ethan questions to startswithabang at gmail dot com!