Ask Ethan: Can we fix the worst prediction in all of science?

Although we don’t often think about it, the world of science is split in two. We have theorists, on the one hand, who strive to tease observable, measurable predictions out of our best models and ideas concerning the Universe. On the other hand, there are experimentalists and observers, who seek to perform those key tests of reality and to determine whether the theories we have accurately describe reality, or whether we’re in need of something more than our current understanding. Each time we perform a new test, or look at the Universe in a fundamentally different or more precise way than ever before, we bring these two worlds together, allowing nature itself to become the arbiter of what we deem as our best approximation of what is real and true.

But sometimes, our theoretical predictions turn out to be nonsensical, and what we observe and measure turns out to be humbling and surprising. In the worst case scenario, our predictions and observations will conflict by enormous amounts, leaving us completely puzzled. It’s precisely that problem that we face when it comes to the zero-point energy of empty space, also known as vacuum energy or the cosmological constant problem. In fact, the cosmological constant problem has the dubious honor of being known as “the worst prediction in all of science,” and that’s what Steve Gulch wrote in to ask about, inquiring:

“Has the worst prediction in all of science, of the cosmological constant been resolved? What about this proposal [by Bob Klauber]?”

The cosmological constant problem isn’t just one problem; it’s actually multiple problems all in one. Here’s what’s going on, as well as where we are on the path to resolving it.

An animated look at how spacetime responds as a mass moves through it helps showcase exactly how, qualitatively, it isn’t merely a sheet of fabric. Instead, all of 3D space itself gets curved by the presence and properties of the matter and energy within the Universe. Space doesn’t “change shape” instantaneously, everywhere, but is rather limited by the speed at which gravity can propagate through it: at the speed of light. The theory of general relativity is relativistically invariant, as are quantum field theories, which means that even though different observers don’t agree on what they measure, all of their measurements are consistent when transformed correctly.

The origin of the cosmological constant problem goes all the way back to Einstein himself, back when he was first formulating his general theory of relativity. Einstein had already come to understand how a great many things worked within his theory:

• he knew how distances (lengths) and durations (times) transformed between different frames of reference,
• he understood that space and time were not separate entities, but rather were woven together into a four-dimensional fabric,
• that gravitation was indistinguishable from any other form of acceleration to the observer,
• but that it was the presence and distribution of matter and energy that dictated how spacetime curved, evolved, and either expanded or contracted.

It was in fact that last point — where Einstein realized that a Universe that was uniformly filled with matter, radiation, or any form of energy could not be stable and static, but must either expand or contract — that kept Einstein up at night when he was putting his greatest theory together. Einstein, like many of his contemporaries, assumed that our Universe was stable, static, and eternal, and neither expanded nor contracted. But according to general relativity, an initially static Universe that was uniformly filled with matter or radiation would contract and collapse, and therefore, Einstein needed something to counteract that.

The only mathematically consistent “thing” he could add that would do so was a cosmological constant: something that behaved as though it were a form of energy intrinsic to space itself. Thus, the idea of a cosmological constant was born.

A mural of the Einstein field equations, with an illustration of light bending around the eclipsed Sun: the key observations that first validated general relativity four years after it was first theoretically put forth: back in 1919. The Einstein tensor is shown decomposed, at left, into the Ricci tensor and Ricci scalar, with the cosmological constant term added in after that. If that constant weren’t included, an expanding (or collapsing) Universe would have been an inevitable consequence.

It was only a few years later, in the late 1920s and early 1930s, that it was shown that the Universe isn’t static and stable, but rather is expanding. Einstein could have predicted this if he hadn’t resorted to the ad hoc introduction of the cosmological constant; this is why it was called his greatest blunder later in his life. The Universe was expanding, not static and stable, and thus the need and motivation for the cosmological constant had evaporated. For years and even decades, it looked like things would remain that way.

But a new development came about in the middle of the 20th century that began to change the story: quantum field theory arrived on the scene. Not only were the quanta comprising matter and radiation subject to the strange, counterintuitive laws of quantum physics — e.g., inherent uncertainties, fluctuating energy states, wave-like behavior, exclusion rules, forbidden transitions, etc. — but the fields that underlied those interactions:

• the electromagnetic field,
• the field describing the weak nuclear force,
• and the field governing the strong interactions,

were also inherently quantum in nature. Phenomena such as the Lamb shift, the Casimir effect, and the Schwinger effect all demonstrated that quantum fields do, in fact, carry energy, and like many quantum systems, it wouldn’t necessarily be true that the “lowest energy state” that they could occupy corresponded to a zero energy state. Like many quantum systems, perhaps there was a positive, non-zero energy state that even empty space itself would possess.

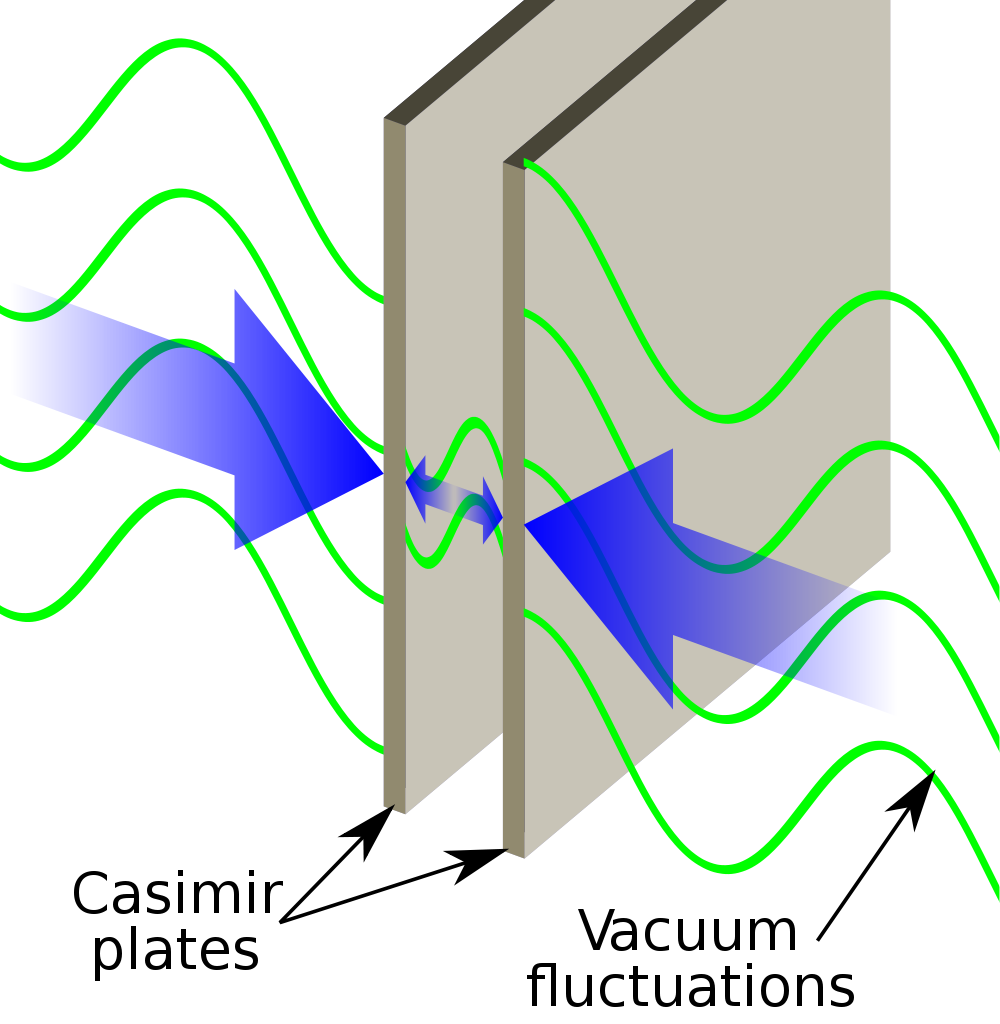
The Casimir effect, illustrated here for two parallel conducting plates, excludes certain electromagnetic modes from the interior of the conducting plates while permitting them outside of the plates. As a result, the plates attract, as predicted by Casimir in the 1940s and verified experimentally by Lamoreaux in the 1990s. The extra restrictions on the type of electromagnetic waves that can exist between the plates can be derived in various quantum field theories.

But how could we calculate it?

Our field theory methods gave only nonsense answers. If you attempted to calculate the contributions of various Feynman diagrams, a tool commonly used in perturbative expansions within the context of quantum field theory, each individual term would lead to enormous contributions: dozens or even more than 100 orders of magnitude greater than would have been physically possible. Remember, our Universe is observed to be many billions of years old, and a Universe that had a zero-point energy, or an energy inherent to space, that was too great in magnitude would either recollapse in just a fraction-of-a-second or would expand away so quickly that not even a single atom, atomic nucleus, or even a proton could have formed.

In fact, if you make a naive order-of-magnitude estimate for how large this zero-point energy inherent to space should fundamentally be, quantum field theory tells you that three of our fundamental constants should come into play:

• Planck’s constant, or ℏ,
• the gravitational constant, or G,
• and the speed of light in a vacuum, or c,

and that the way they should come together would give you something in units of energy to the fourth power.

The way to get an energy scale out of this combination of constants is √(ℏc⁵/G), and that leads to the Planck energy: 1.22 × 10²⁸ eV, or electron-volts. Take that to the fourth power, and you get approximately 10¹¹² eV⁴.

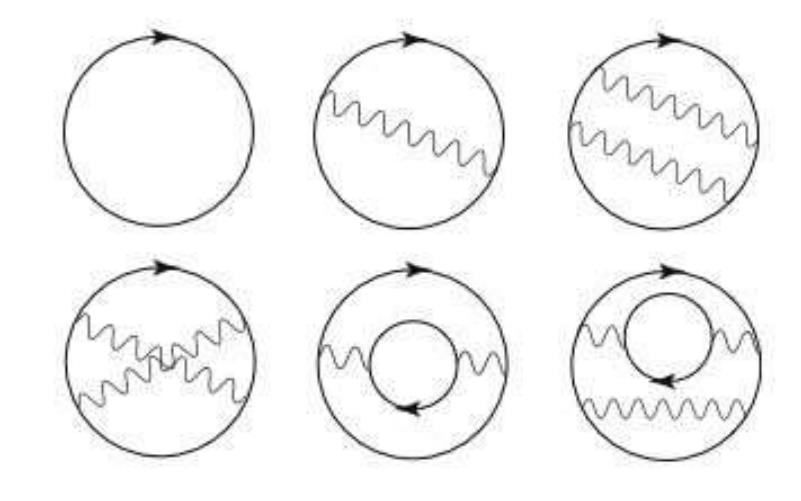
A few terms contributing to the zero-point energy in quantum electrodynamics. The development of this theory, due to Feynman, Schwinger, and Tomonaga, led to them being awarded the Nobel Prize in 1965. These diagrams may make it appear as though particles and antiparticles are popping in and out of existence, but that is only a calculational tool; these particles are virtual, not real, even though the energy contributions that they make to the zero-point energy of space may indeed be real. We do not have an explanation for the extremely low observed value of our Universe’s vacuum energy.

But this leads to exactly the problem we just mentioned: such a value for the cosmological constant would have destroyed the Universe almost immediately after its birth. If it were truly of a value like 10¹¹² eV⁴ in the positive direction, the Big Bang would have led to a colossally large, relentlessly exponential expansion, driving every quantum away from every other so quickly that the Universe would be essentially emptied out with every ~10^-40 seconds that elapsed. Similarly, if it were truly of that same value but in the negative direction, the Universe would have recollapsed literally the instant the Big Bang occurred: after merely ~10^-43 seconds had elapsed.

A lot of people in the field assumed that our inability to perform these quantum field theory calculations — and to get such remarkably large answers each time we try to calculate even a single term or contribution to the zero-point energy of empty space — simply meant that either:

• we didn’t know how to do these calculations appropriately, and that the “real answer” must be zero for some yet-to-be-determined reason,
• or that there was some new symmetry that we hadn’t yet discovered that would “cancel out” all of these seemingly unique terms that arose in our conventional Standard Model.

In other words, the very fact that our Universe existed, and that it existed without a tremendous, catastrophic cosmological constant within it seemed to indicate that it might be zero, and that it was up to us to figure out why.

In the Standard Model, heavy particles like the top quark contribute to the Higgs mass through loop diagrams like the one shown at the top. If there’s a comparably-massed superpartner particle, as shown in the lower image, it could cancel out that coupling, preventing the mass of the Higgs (and other Standard Model particles) from becoming too large, and posing a potential solution to not just the hierarchy problem, but the puzzle of why the cosmological constant doesn’t take on an extremely, unphysically large value.

The proposals that our question-asker for the week put forth, here and here, fall into that first category: attempts to explain why this thing that we’d naively calculate to be huge is actually zero, but the jury is still out on whether this speculative scenario actually solves that aspect of the puzzle or not. Part of the reason that physicists remain so excited about supersymmetry, despite the extraordinary lack of experimental evidence supporting it, is that it is one of the most promising theoretical schemes to impose a symmetry that could cancel out all of the contributions of the Standard Model to the zero-point energy of the Universe. Despite all of the progress we’ve made in theoretical physics, including in understanding the Standard Model and everything that it brings along with it, we have yet to find a compelling resolution to the cosmological constant problem.

In the mid-1980s, physicist Steven Weinberg was thinking about this problem, and was thinking about it in the context of not just cosmic inflation — which creates an incredibly large number of “pocket” or “baby” Universes — but in the context of string theory as well. Cosmic inflation, which precedes and sets up the hot Big Bang, represents a phase of the Universe where there was a large, constant amount of vacuum energy, and in string theory, the zero-point energy of empty space is a reflection of what’s known as the expectation value of the quantum vacuum. What Weinberg did next was invoke a principle that’s often misused (but remains very popular) in theoretical physics: the anthropic principle.

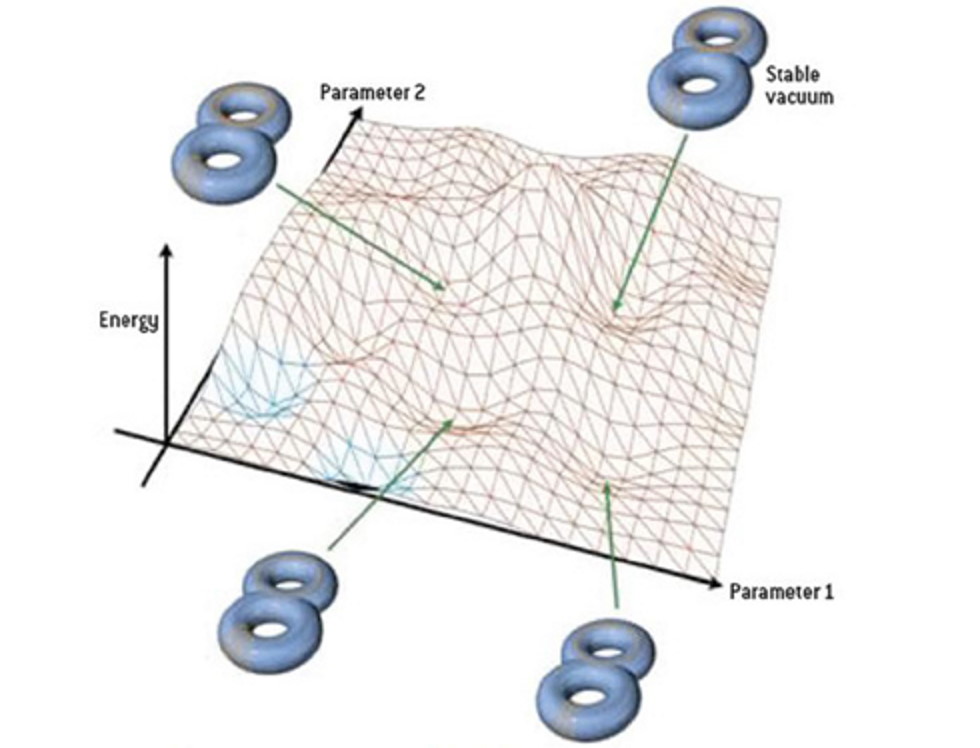
The string landscape might be a fascinating idea that’s full of theoretical potential, but it cannot explain why the value of such a finely-tuned parameter like the cosmological constant, the initial expansion rate, or the total energy density have the values that they do. Each “pocket” of the string landscape has its own unique vacuum expectation value, which corresponds to a value for a fundamental constant in the Universe.

Weinberg recognized that in the context of string theory, there’s an infinite landscape of all possible values that the zero-point energy of space could take on. In this inflationary multiverse of new, baby universes, each with their own Big Bang, all possible values will be taken on so long as there are enough “universes” created to fully occupy (or sample) the different possible quantum states. And therefore:

• all possible values will be taken on by the zero-point energy of the quantum vacuum in some pocket, baby universe,
• that in most of those universes, the value of the zero-point energy will be too large to admit the existence of observers,
• and since we exist and are observers, we must therefore occupy a pocket of the multiverse that took on one of these smaller values.

Weinberg used this line of reasoning, way back in 1987, to therefore predict that the cosmological constant that we observe should not be zero, but should be very small in magnitude but finite in nature, just more than 100 orders of magnitude smaller than the naive theoretical prediction of ~10¹¹² eV⁴. We exist, therefore the Universe must admit the existence of observers, therefore the pocket of the multiverse we live in should be such a pocket where the cosmological constant is small enough to not eliminate the possibility of observers.

When the evidence supporting dark energy’s existence in 1998 came in, many viewed it not only as a revolution in cosmology, but as indirect evidence supporting Weinberg’s reasoning, and a validation of the idea of the string landscape.

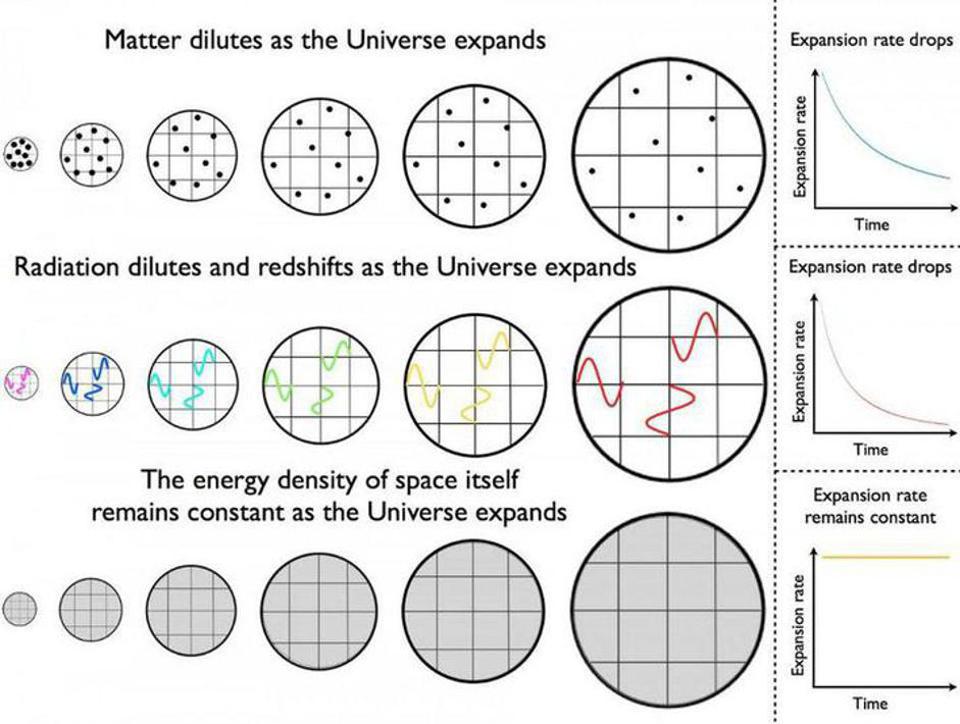
While matter and radiation become less dense as the Universe expands, owing to its increasing volume, dark energy is a form of energy inherent to space itself. As new space gets created in the expanding Universe, the dark energy density remains constant. However, we still lack an explanation for why the value of the dark energy density takes on the small, positive, non-zero value that it does.

But, of course, most people remained unconvinced of this line of thought. Sure, Weinberg’s reasoning led us to what turned out to be the correct answer, but did we get the right answer for the right reason, or did dark energy just happen to exist, and exist with the value we observed it to have, for some completely different reason?

There’s a big reason to disfavor Weinberg’s logic, however: we know what the energy scale of inflation is, because we have, from observations of the CMB, an upper limit to how hot the Universe could have possibly gotten at the hottest part of the hot Big Bang. And while those energies are incredibly high, they are a few orders of magnitude still below both the string scale and the Planck scale: it is in fact the first point that arises as far as observational tests of inflation are concerned. Therefore, unless you invoke some new, hitherto unseen physics during a pre-inflationary state, there is no way to conceivably have the expectation value of the quantum vacuum be set by some process that occurs during inflation.

The truth of the matter is that we still do not know how to calculate the quantum vacuum in any way, and that while Weinberg’s reasoning did indeed give us the correct answer, it may also serve as an example of the inverse gambler’s fallacy. The truth is that we still don’t know why the cosmological constant has the value that it does.

This to-scale diagram shows the relative masses of the quarks and leptons, with neutrinos being the lightest particles and the top quark being the heaviest. No explanation, within the Standard Model alone, can account for these mass values. We now know that neutrinos can be no more massive than 0.45 eV/c² apiece, meaning that the difference between a neutrino’s mass and an electron’s mass is more than three times as large as the difference between the electron’s mass and the top quark’s mass.

There is, however, a very suggestive thing that many have noticed: that naive prediction of what the value of the cosmological constant should be, which is an energy given by ~√(ℏc⁵/G) raised to the 4th power, is how we arrived at the absurdly large value of ~10¹¹² eV⁴. That energy is known as the Planck energy, and that’s what √(ℏc⁵/G) represents.

But what if we used a different value for energy instead?

For example, if instead of the Planck energy, we used the rest mass energy of the Higgs boson, which occurs at the electroweak symmetry breaking scale, we’d get a much smaller value of just ~10⁴⁴ eV⁴. If we put in the rest mass energy of an even less massive particle, like the electron, we’d get an even smaller value: around ~10²³ eV⁴.

But the actual, observed value of dark energy corresponds to an energy density for the cosmological constant that’s more like ~10^-10 eV⁴, which is so different from the naive prediction of ~10¹¹² eV⁴ that we do indeed note that it’s the worst prediction in the history of theoretical physics. But if instead we put in something whose energy is the Planck energy, √(ℏc⁵/G), raised to the 4th power, we put in something that was more like 0.003 eV in energy and raised this to the 4th power, we’d get a cosmological constant whose predictions matched observations. Interestingly, there are two things in physics that could have that energy:

This 2018 plot shows the exclusion limits on axion abundances and couplings, under the assumption that axions make up ~100% of the dark matter within the Milky Way. Both the KSVZ and DFSZ axion exclusion limits are shown. Note that if the axion mass is used to calibrate the “energy scale” expected for dark energy, it makes a suggestive candidate.

Still, no one has made an end-to-end theory that can explain why the value of the cosmological constant is so small compared to the naive theoretical predictions. Many still assume that there is some hitherto unknown explanation for a cancellation of all the expected Standard Model terms, with some small, additional contribution giving our Universe a positive, non-zero value for the vacuum expectation value of empty space.

• It could be related to neutrino masses, which themselves still lack a full explanation.
• It could be related to the hypothetical axion, or to the underlying (theoretically, Peccei-Quinn-like) symmetry that gives rise to axions or axion-like particles.
• Or it could be due to a new chameleon-like or symmetron-like field, or a modification to Einstein’s law of gravity, even though direct experiments rule many of those scenarios out.

All of these scenarios, unfortunately, remain speculative. However, by taking stock of what we know right now, we can recognize that the “cosmological constant” problem is actually two problems in one. The first aspect of the problem is that we don’t know how to avoid the cosmological constant taking on a huge value: a value that’s far too unphysically large to be compatible with the Universe we inhabit. Something that is not yet known must exist as the underlying explanation for enabling our Universe to exist as it does. And second, we know that whatever happens to cancel the naive, too-large value out for the cosmological constant must also leave you not with “zero,” but with a small, positive, non-zero value consistent with the dark energy we actually have in our Universe.

Most proposals purporting to explain dark energy address only one of these aspects, but in order to solve the puzzle of the “worst prediction in all of physics,” we’ll have to explain them both. And so far, both of them are still very real — and very unsolved — problems that we still face.

Send in your Ask Ethan questions to startswithabang at gmail dot com!